The principal axes of a sampled ellipse are the ellipse's principal axes
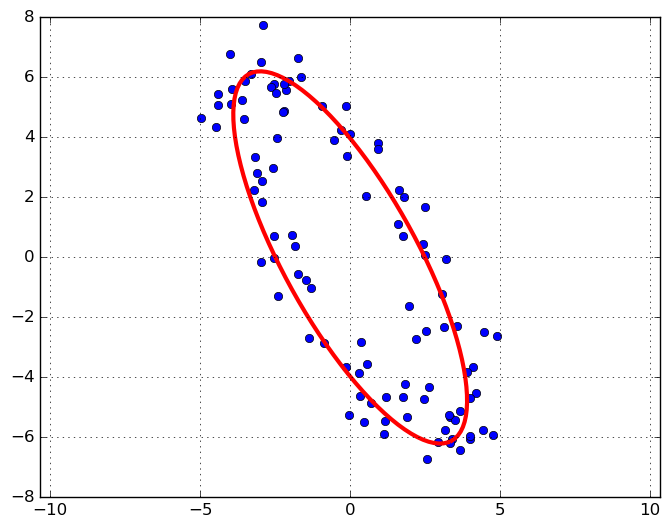
What would you expect if you sampled points from an ellipse and used PCA to find the principal components? We know from a separate post that the principal component directions and magnitude are the eigenvectors and eigenvalues of the scatter matrix, which itself is the maximum likelihood estimate of the covariance matrix. Intuitively, we expect that directions given by PCA should match. This is a sort “sanity check” calculation, but it also is useful if you want to fit an ellipse to scattered data because this tells you via PCA how wide the ellipse should be along its major and minor axes.
The scatter matrix for points sampled from an ellipse
We ignore the rotation and translations components since these can be factored in easily afterwards. So, let’s sample from the parametric form of an ellipse: $[a\cos(2\pi t), b\sin(2\pi t)]^T$. Recall that the parameters, $a$ and $b$, represent the distances from the origin in the $x$ and $y$ directions respectively. We sample uniformly in $t$ so that the $k$th sample for sample of size $N$ is
\[\mathbf{x}_k = \begin{bmatrix} a\cos(2\pi k /N) \\ b\sin(2\pi k/N) \end{bmatrix}, \;\; k=0,1,\ldots,N-1\]The data matrix is:
\[X = \begin{bmatrix} \mathbf{x}_0^T \\ \vdots \\ \mathbf{x}_k^T \\ \vdots \\ \mathbf{x}_{N-1}^T \end{bmatrix}\]So then:
\[\frac{1}{N} X^TX = \frac{1}{N} \sum_{k=0}^{N-1} \mathbf{x}_k \mathbf{x}_k^T = \frac{1}{N} \sum_{k=0}^{N-1} \begin{bmatrix} a^2 \cos^2(2\pi k /N) & ab \cos(2\pi k/N)\sin(2\pi k/N) \\ ab \cos(2\pi k/N)\sin(2\pi k/N) & b^2 \sin^2(2\pi k /N) \end{bmatrix}\]Each component in the matrix is just a Riemann sum. This says if $N \to \infty$, then:
\[\frac{1}{N} X^TX \to \begin{bmatrix} a^2 \int_0^1 \cos^2(2\pi x) dx & ab \int_0^1 \cos(2\pi x) \sin(2 \pi x) \\ ab \int_0^1 \cos(2\pi x) \sin(2 \pi x) dx & b^2 \int_0^1 \sin^2(2\pi x) dx \end{bmatrix} = \begin{bmatrix} \frac{a^2}{2} & 0 \\ 0 & \frac{b^2}{2} \end{bmatrix}\]What’s more, is that we don’t even need to let $N \to \infty$. In fact, the equality:
\[\frac{1}{N} X^TX = \begin{bmatrix} \frac{a^2}{2} & 0 \\ 0 & \frac{b^2}{2} \end{bmatrix}\]holds for any $N$ so long as we exactly sample points from an ellipse. One can see that this equality holds independent of $N$ by using, for each matrix component, the complex exponential definition of $\cos$ and $\sin$, and seeing that each sum is a geometric.
Ellipse fitting
So let’s say our points aren’t sampled exactly from ellipse, but we’d like to use PCA to fit an ellipse to these points. Typically PCA finds the singular value decomposition of $X/\sqrt{N}$ so that $\frac{1}{N} X^TX = VS^2V^T$. To fit an ellipse to scattered data, we can simply set $a = \sqrt{2}s_1, b = \sqrt{2}s_2$, and then rotate the ellipse to the direction of the first right singular vector. Here’s an example: