A relationship between accuracy and the AUC score
In this post, I derive a relationship between analytic accuracy and $\text{AUC}$ score. These quantities are introduced and derived in a previous post. I admit that the relationship is somewhat nonintuitive, so this post is mostly just for fun. On the other hand, the existence of the relationship is interesting in its own right.
Notation and preliminaries
Recall that for a given threshold, $t$, the analytic accuracy is the sum of probabilities:
\[\begin{align*} \text{ACC}(t) &= P(T \gt t , Y=1) + P(T \lt t , Y=0) \\ &= P(T \gt t | Y=1)P(Y=1) + P(T \lt t | Y=0)P(Y=0) \end{align*}\]where $T \in [0,1]$ is the output of a trained classifier (for which, we must choose a threshold to decide which class the output belongs), and $Y \in \{0,1\}$ is the ground-truth class label.
As a matter of notational convenience, denote $F_j(t) = P(T \lt t | Y=j)$ and $p = P(Y=1)$. Assume densities exists, and denote $F_j’(t) = f_j(t) = p(t | Y=j)$. So then,
\[\text{ACC}(t) = (1-F_1(t))p + F_0(t)(1-p)\]Recall that the analytic form of the AUC score can be given by the integral:
\[\begin{align*} \text{AUC} &= \int_0^1 (1-F_1(t)) f_0(t) dt \\ &= \int_0^1 F_0(t) f_1(t) dt \\ \end{align*}\]with the second equality owing to a simple integration by parts.
Relating accuracy and AUC
Ok. So notice that accuracy is a function of the threshold, and involves the cumulative distribution functions. Meanwhile, the $\text{AUC}$ metric also involves the conditional cumulative distribution functions (and densities), but doesn’t depend on the threshold because it is integrated out. So it seems that the only obvious thing to do (in order to relate accuracy and the $\text{AUC}$) is to integrate accuracy.
In particular we’re going to integrate $\text{ACC}(t)$ against the density, $f(t) = pf_1(t) + (1-p)f_0(t)$:
\[E[\text{ACC}(T)] = \int_0^1 \text{ACC}(t) f(t) dt\]This is the expected accuracy if we were to choose the threshold based on the distribution of the classifier. So, nature gives us some $X$, we run it through our classifier to obtain $T$, and then we measure the accuracy using this value as a threshold. Do this a whole bunch of times, and this is the expectation above. Why would you do this? I don’t know! But it’s simply our only real option in order to relate accuracy and AUC. Continuing with the expression above:
\[\begin{align*} E[\text{ACC}(T)] &= \int_0^1 \text{ACC}(t) (pf_1(t) + (1-p)f_0(t)) dt \\ &= p \int_0^1 \text{ACC}(t) f_1(t) dt + (1-p) \int_0^1 \text{ACC}(t) f_0(t) dt \\ &=: (1) + (2) \end{align*}\]So then,
\[\begin{align*} (1) &= p \int_0^1 ( (1-F_1(t))p + F_0(t)(1-p) ) f_1(t) dt \\ &= p^2 \int_0^1 (1-F_1(t)) f_1(t) dt + p(1-p) \int_0^1 F_0(t) f_1(t) dt \\ &= \frac{1}{2} p^2 + p(1-p) \text{AUC} \end{align*}\]Similarly, one finds that \((2) = \frac{1}{2} (1-p)^2 + p(1-p) \text{AUC}\). Combining these yields:
\[\begin{align*} E[\text{ACC}(T)] &= \frac{1}{2}\left( p^2 + (1-p)^2 \right) + 2p(1-p) \text{AUC} \\ &= p(p-1) + \frac{1}{2} + 2p(1-p) \text{AUC} \\ &= p(1-p) \left( 2\text{AUC} - 1 \right) + \frac{1}{2} \end{align*}\]Note that the quantity, $p(1-p)$, is the variance of the class label, $Y$. So the expected accuracy when the threshold is determined by a random draw from the classifier’s output is proportional to the the variance of the label times the $\text{AUC}$ score (plus some scaling and additive constants). Here’s the the plot of this quantity as a function of $p$ for various $\text{AUC}$s:
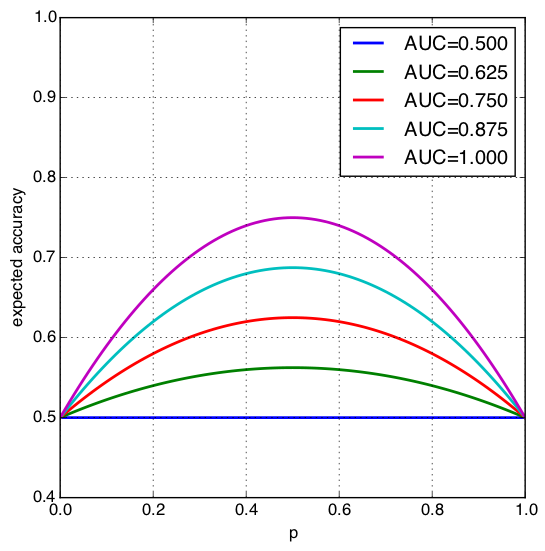
Some things to notice:
- When $\text{AUC}=1/2$, the expected accuracy is also $1/2$, no matter the balance of the class labels (determined by $p$). This makes sense if you consider that an $\text{AUC}=1/2$ may arise from an ROC curve that represents a classifier that only guesses.
- The expected accuracy is $1/2$ whenever $p=0$ or $p=1$. At first this doesn’t seem to make sense: why would the expected accuracy be the worst when the the label is perfectly non-random. In this case, the conditional distributions don’t make sense. This essentially means $\text{ACC}(t)=P(T \lt t)$ or $\text{ACC}(t)=P(T \gt t)$ for $p=0$ or $p=1$ respectively. So, $E[\text{ACC}(T)]$ in both cases is the expected value of a CDF or complementary CDF, which is always $1/2$ in the continuous case.
- The maximum expected accuracy is only $3/4$. I am not able to explain this in any meaningful way!